Compound interest was once allegedly described by Albert Einstein as “the eighth wonder of the world” – it’s no wonder then that the day I understood the phenomenon of ‘compound interest’ and more generally ‘compounding’ was the day I realised that becoming rich isn’t something that’s impossible to do or reserved solely for the super-high earners of the world but rather something anybody can do if they understand and take advantage of compounding.
Stock market investing does not technically benefit from ‘compound interest’ as you do not earn interest on stocks & shares investments. However, stock market investments do benefit from compounding i.e. you earn returns on the returns previously accumulated on your investments in a snowball effect.
Don’t worry if this doesn’t come intuitively, throughout the below post we will be diving into exactly what compound interest is, the formula to calculate it (and how you can use online calculators to do the maths for you) and run through some practical examples which demonstrate the power of compounding as I once again dust off the old Excel spreadsheet.
What is compound interest?
Compound interest refers to the interest earned, plus the interest earned on the interest that has previously accumulated over time. For example, £100 at 5% interest is £105 after 1 year and £110.25 after 2 years. The growth increases over time as you start to earn interest on the interest.
So we’ve established so far that compound interest is not only the interest on your investments but also the interest on that interest. For many people, this will be easier to see visually, so here we go:

As you can see, over the course of 5 years, in this example we only invested once – £100 on the first day. After that, we let our investment sit and grow (by 5% per year). At the end of the 5 years, our investment is worth £127.63, so we have investment returns of £27.63 in total.
Our principal is the £100 initially invested and we are earning interest at 5% a year, so with regular interest, we would expect to earn £5 interest (5% * £100) each year, right? If that were the case, over 5 years we would earn interest of £25 (5 years * £5 per year) and our total investment would be £125 at the end of the 5 years. However, as the table above shows, our total investment isn’t £125 but rather £127.63 and this difference (although small in this example) is the power of compounding.
Another way of looking at this is to look at the ‘investment returns’ column, each year, our investment return is bigger than the year before because we are earning 5% interest on a larger starting balance which now contains the previous year’s interest.
Compound interest is otherwise known simply as ‘compounding’, ‘interest on interest’ or ‘the future value of money’.
In our example above, compounding interest was responsible for increasing our investment by only £2.63 (£127.63 – £125) but as you start to work with larger numbers, the impact is magnified. It’s for this reason that compounding is the single most important concept within personal finance – if you invest early and allow your investments to grow over a long enough time period, eventually, you may just have enough to declare yourself financially independent.
How does the maths of compound interest work?
Let’s take a look at another example, but this time with some proper numbers attached. Let’s say you were in a position to invest £10,000 on January 1st every year between the ages of 20 and 60, how much would your investment portfolio be worth on retirement at age 60?
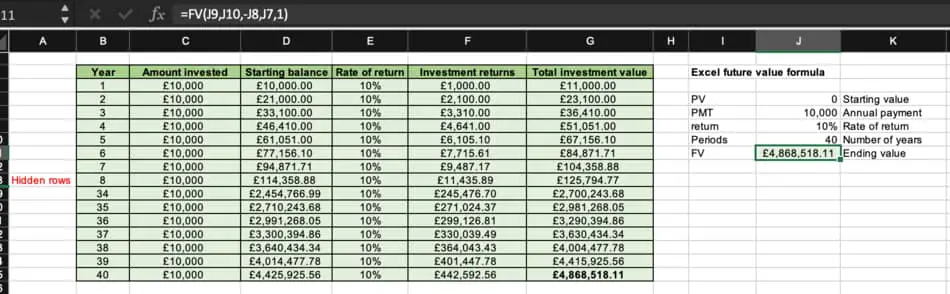
As you can see, I have hidden the rows between years 8 and 34 so we can see everything on one screen.
Answering the above question, if you invested £10,000 at the start of each year between the ages of 20 and 60 and assumed 10% returns per year, your investment account would be worth £4,868,518.11 by the end of the final year. Yes, £4.9 million.
The assumptions I’ve used here are as follows:
Present value: £0 – this means before we start investing, our investment account is worth £0 prior to the first payment.
Payments: £10,000 per year – as per above, on January 1st every year, we deposit £10,000 into our account.
Rate of return: 10% – The S&P500 has annualised investment returns of 10% (to the nearest whole number) – more on this assumption later.
Periods: 40 – We are investing once a year between the ages of 20 and 60.
As you can see in the above spreadsheet – in the final year, our total investment is worth £4.9 million and we have only contributed £400,000 of our own money (40 years * £10,000 per year). That means the returns of 10% per annum we earn via compounding has contributed to £4.5 million of this final value.
On the right-hand side of the image above, I have used excels future value formula to calculate the same thing which not only tells me my maths was correct but also more clearly shows each of the data inputs i.e. the number of periods, assumed return, the value of each annual deposit and the starting point.
Interestingly, if we changed our expected return from 10% to 5%, this has a huge impact on our ending balance as it now becomes £1.3 million. Still a lot of money and still huge returns due to compounding (£900k) but significantly smaller than our balance using 10%.
Hopefully, now the power and influence of compounding are clear.
The compound interest formula explained
This is easy to work out using Excel’s ‘=FV’ function but let’s take a look at the basic compound interest formula itself.
Unlike our example above, this formula doesn’t work with recurring payments (£10,000 in our example above) but can be used to tell you what an initial starting balance will be after being compounded for 40 years. So let’s assume this time we have £10,000 invested as our starting point and we do not contribute any more to it. What will it be worth in 40 years time?
The formula for compound interest without recurring payments is: FV = PV( 1+ R/N) ^ NT
Where:
FV = future value – our ending balance (what we are trying to calculate)
PV = present value – our starting point balance (£10,0000 in our example)
R = rate of return % – the return we expect on our investments (10% in our example)
N= number of times interest applied per period i.e 1 for annually, 12 for monthly (1 in our example above)
T = Number of time periods elapsed i.e. years (40 in our example)
So applying the formula of FV = PV( 1+ R/N) ^ NT to our example we get:
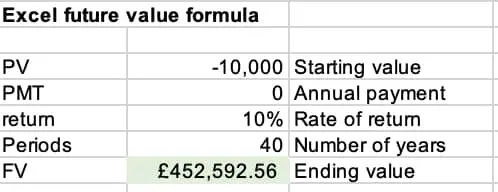
FV = £10,000 (1+ 10% / 1) ^ 1*40 = £452,593.
This is also what our Excel formula gives:
Compound interest calculator
If you want to test this out for yourself but don’t fancy giving the formula above a go, the easiest ways are to either use the Excel formula as I have above by simply typing “=FV” into Excel and then following the prompts or by going to an online compound interest calculator.
For example, this online compound interest calculator by thecalculatorsite.com is very good. Just be careful over selecting monthly/annual compounding periods which can be a common mistake when making the calculations.
Does compound interest work when investing in stocks?
Compound interest / compounding is applicable to investing in stocks but we need to be careful with what we call it here because technically speaking stocks do not earn ‘interest’. Interest is made on cash accounts or fixed income products. Stock investments grow via capital appreciation of the share price and via reinvestment of dividends. Whilst these things do ‘compound’ over time, it is not technically ‘compound interest’.
Capital appreciation
Capital appreciation of stocks is simply the value of your investments increasing because the share price of the underlying companies have increased. For example, let’s say your whole portfolio is made up of shares in a single company – Company X. If on the day you bought shares in company X the share price was £2.00 per share and on today’s date it is £2.50 per share, that means your shares have appreciated by 50p per share. So if you bought 1000 shares, you would have initially spent £2000 (£2 per share * 1000 shares) and it is now worth £2,500, so you have received returns of £500.
It’s important to note that you have not actually earned anything at this stage – whilst the shares are still in your investment account, these £500 gains are ‘unrealised’ until they are sold. If you sold them on this day, you would make a ‘realised gain’ of £500.
It’s also worth noting that the share price could easily go down e.g. you bought at £2.00 per share and they are now worth only £1.00 per share. In our example above, you would have an unrealised loss of £1,000 as you bought for £2,000 and they are now only worth £1,000. As long as you don’t sell at this point, this loss is not realised and you can simply wait for if and when the share price increases again.
This is also a good example of why your investment portfolio should be more diversified than a single companies shares but more on this later.
Dividends
A dividend is basically just a sum of cash a company pays out to its investors (shareholders) on a periodic basis, usually annually as a reward to the investors for their ownership. Dividend payments are typically more common for established companies as younger companies are not in a financial position to give back cash to investors as they need the cash to reinvest into their business.
When you and I invest in an investment product such as a mutual fund, we are essentially buying small portions of company shares of all of the companies that the mutual fund invests in. For example, there are a number of S&P 500 funds that invest in the 500 largest companies listed on the stock exchange in the United States. That includes companies like Coca Cola and PepsiCo who both pay out dividends.
When these companies pay out dividends, the investors in the mutual fund get their proportionate share based on how many shares of that company they own. This can either be taken as cash paid directly to your bank account or automatically reinvested into more units of the fund.
This is the difference between an ‘INC’ and ‘ACC’ fund which stands for ‘income’ and ‘accumulation’ respectively. Income-based funds pay you your dividends out as income whilst accumulation funds reinvest on your behalf. The accumulation fund is the better for growth and to benefit from compounding as similar to our example above, with this dividend income, we buy more units of the fund which in turns gets us more dividends in the future and so on.
For more on the difference between ACC and INC funds, check out my post on The difference between accumulation and income funds (ACC vs INC)
What is dollar cost averaging and how can it help you?
Put simply, the concept of dollar-cost averaging is an investment strategy that means you purchase periodically (say every month) to reduce the volatility associated with investing your money in one single lump sum.
The idea behind this is that if you invest each month rather than say once at the start of the year, sometimes your investments will be prior to the share price going up whilst other times it will be before the share price goes down. By investing more periodically, the theory says you will get the average. If you invested once, you may be investing at a point where the share price is high and on its way down.
One way in which this strategy is beneficial is that it allows investors to be consistent. If you are contributing to your investment account every month, that stands you in very good stead to benefit from compounding over the long term.
This strategy is not without its detractors however as some argue that simply having the money invested for a longer period of time will enable more time for the investments to grow via the reinvestment of dividends.
As an example, if we had £12,000 to invest, would we be better investing all of it on January 1st or splitting it and investing £1,000 each month for a year (dollar-cost averaging)?
If we assume our investments will receive total returns of 10% per year (including capital appreciation and dividend income) our investments in both situations would look as per the below:
Lump-sum method value at end of the year: £11,000. (£10,00 investment, 10% returns)
Dollar-cost averaging method at end of the year: £10,559 (£1,000 recurring deposit at start of each month, 10% returns annually)

As you can see, simply due to the £10,000 being in the market for the full year, the lump-sum method gives us an expected greater end value. Dollar-cost averaging supporters would likely say that this doesn’t take into account the fluctuations in share price and investment returns throughout the year which is true but my personal preference adheres to the saying ‘time in the market > timing the market’.
What stops investors from getting rich with compound interest
We’ve seen above that accumulating significant wealth is possible via compounding. However, as humans, we are all susceptible to human fallibilities, not least when it comes to investing.
Fear of loss
The first and most prevalent fallibility is simply the fear of loss. To benefit the most from compounding, you have to be willing to buy and hold investments for the long term. If at the first sign of trouble an investor sells their shares, they are doing themselves a huge disservice.
Not only would the investor “sell low” i.e. when the share price is at a comparably low price and therefore lock in a ‘realised loss’, but they would also miss out on the benefits of years of compounding.
If an investor knows this and can comfortably ride out the periods of time when the market is not favourable, they will be in a much better position for the long term.
Greed
Similarly, greed can play a big part when it comes to investing your money. The strategy which stands the most to gain from compounding is one where you buy investments and hold them for the long term to allow for years of compounding. This is not flashy and the returns are typically in the 0-10% per year range which doesn’t typically set pulses racing. However, as you’ve seen with the example above, over the long term, this strategy leads to huge increases in wealth over time.
What happens, however, if you hear from a friend about a hot stock tip? Do you stay the course with your secure, long-term plan or do you get sidetracked? Greed may convince you it’s a good idea to sell your investments in favour of piling your money into this poorly researched tip.
For more information on common investing fallacies, check out this article by medium.com.
The earlier you start, the greater the benefits of compounding
As should be clear by now, the earlier you start investing (regardless of whether in the stock market or just in a cash account), the greater the benefits of compounding in the long term.
Let’s say I have two friends – Kieran and Hector. Both plan to retire when they are 60. Hector doesn’t think about investing at all whilst young but has amassed a high salary and at age 50 starts investing significantly – £25,000 per year. Keiran on the other hand, cannot command a high salary but from the age of 20 commits to investing just £1,000 per year.
As you can see, in total Kieran invests £40,000 of his money (£1,000 * 40 years) whilst Hector invests considerably more at £250,000 (£25,000 * 10 years). So who do you think retires with the greater stache?
It may surprise you to learn that low-salary but consistent Kieran retires with more (£486,852) than high-salary Hector who only retires with £438,279.
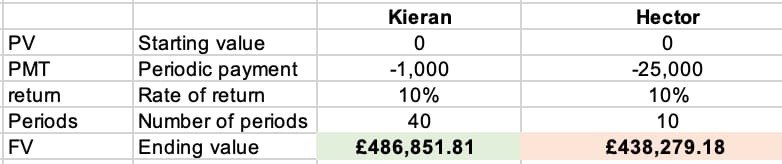
The point of this is to make clear that consistent, long term investing trumps short-term, high value investing and that the earlier you start, the more years you let “your money work for you” to help you get rich over the long term.
Why compound interest can also have negative implications for your finances
The less good news is that compounding works in both ways. So far, we have framed it as a positive in terms of investment returns but the same thing can be true in terms of credit card debt.
Let’s say, for example, you took out a loan for £5,000 which attracts interest at 10%. If you fail to pay the interest, it may get added to the principal and future interest payments are then on the original £5,000 plus the accrued interest. Clearly, this could be disastrous for your personal finance.
Where possible, the easiest solution is to do everything you can to avoid these types of loans (or any debt) unless you are 100% sure you can make your payments on time.
How the concept of compound interest can be applied to other areas of your life
We’ve now gone through compounding in detail when it comes to investments but what’s interesting is the overall concept of compounding can be applied to other areas of your life.
When talking about numbers, we say that compounding is making interest on the interest you have previously earned but what if we thought about this more generally as ‘getting benefits on benefits you have already earned’ whereby I mean benefits in the general sense of the word, not state-paid benefits.
It’s my belief that this can work in any area of your life whether that be your motivation, your health or your productivity. Once you make an improvement of 1% in these areas of your life, next time you take another step forward it’s 1% of the new baseline.
Conclusion
Compounding is, for me, the most important concept in personal finance. Put simply, compounding is the idea that interest that you earn is added to the principal to the point where you start earning interest on interest.
To summarise, compound interest is the interest you earn on previously accrued interest. As the examples above suggest, compound interest can have a transformational impact on your wealth, particularly if you start investing early and are consistent with investment contributions over the long term.
The formula to work out compound interest without recurring payments is FV = PV(1+ R/N) ^ NT but it is usually easier to calculate using Excel’s ‘=FV’ formula or by using one of the many excellent online compound interest calculators.
As always, please remember I am an Accountant, but not your Accountant. In this post (and all of my others) I share information and oftentimes give anecdotes about what has worked well for me. However, I do not know your personal financial situation and so do not offer individual financial advice. If you are unsure of a particular financial subject, please hire a qualified financial advisor to guide you.
This article has been written by Luke Girling, ACA – a qualified Accountant and personal finance enthusiast in the UK. Please visit my ‘About‘ page for more information. To verify my ACA credentials – please search for my name at the ICAEW member finder. To get in touch with questions or ideas for future posts, please comment below or contact me here.
